天堂网www,免费追剧大全在线观看电视剧,97久久精品无码一区二区欧美人 ,日本丰满少妇高潮呻吟

在共振點探查試驗中，細心的工程師會發(fā)現(xiàn)一個困惑，在沒有指定掃頻速度和掃頻方向時，不知道該如何選擇合適的掃頻速度和掃頻方向進行試驗？

這是因為，第一，掃頻速度的大小（快慢）影響共振峰的放大倍數(shù)。理論上講，掃頻速度過快，會丟失一些頻帶比較窄的共振點。好比一個球在凹凸不同帶有洼穴的斜面上滾下一樣，速度比較慢，球就可以滾進每個洼穴和凸點。速度比較快的話，一些小洼穴就不會進去。所以，在設置振動臺掃頻參數(shù)時，盡量放低掃頻速度，不論是線性掃頻還是對數(shù)掃頻，都有利于發(fā)現(xiàn)更多的共振點。第二，隨著向上掃頻（頻率由小到大）并接近共振時，共振點的幅值開始增加，由于振幅和頻率是成反比例的關系，所以幅值的增加導致共振頻率的降低。當向下掃頻（頻率從大到小）并接近共振時，共振正好也向同一方向移動。隨著幅值的增加，共振頻率會降低。所以，掃頻方向和共振頻率移動一致時，掃頻測試就會有更充足的時間采集試驗體的共振峰。

其實，這主要涉及掃頻速度及掃頻方向和振動響應的關系，接下來就詳細地來說明這個復雜關系。假設不用掃頻（掃頻速度為零），直接用試驗體的共振頻率給試驗體正弦定頻加振，試驗體的振動響應會慢慢成長，一定時間加振持續(xù)，試驗體的振動響應飽和（完全共振），振幅達到Q值（Q=1/2ζ），如下圖1所示，

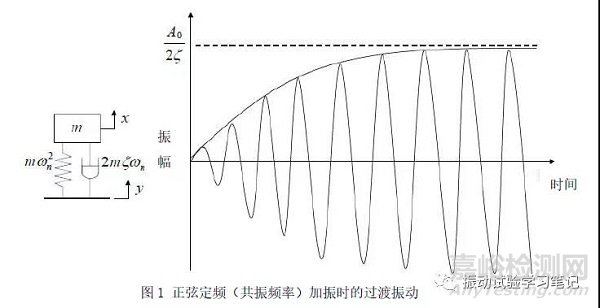
也就是說，達到完全共振需要一定時間，之前的振動稱為過渡振動狀態(tài)。阻尼比ζ，固有角加速度ωn的單自由度振動模型，施加位移

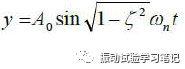
初期位移0及初始速度0，則單自由度的位移x為，

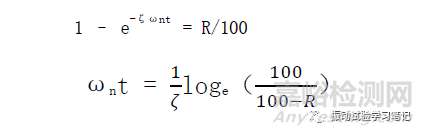
共振頻率正弦振動次數(shù)N=ωnt/2π、ζ（Q值）、R%三者之間的曲線如下圖2，

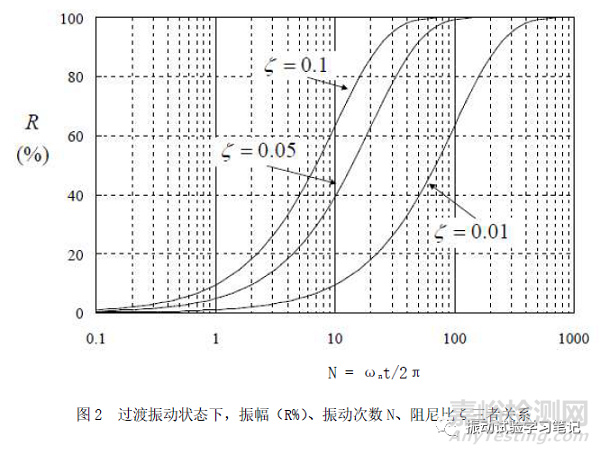
  掃頻試驗時，試驗體的響應也是一個過渡振動狀態(tài)，由于試驗體的Q值和掃頻速度的影響，振動響應會有所變化。下圖3中，橫軸是掃描頻率，縱軸為掃頻速度變化時振動響應的峰值。

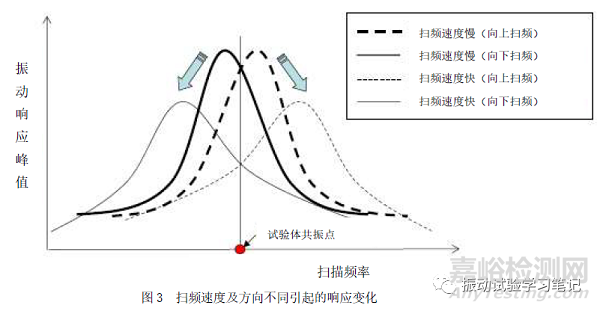
圖中，掃頻速度快速的場合，共振時試驗體的振動響應不能充分，峰值對應掃頻速度變小，且共振點會有所偏移。頻率從小到大掃描時（向上掃頻），共振點大于實際共振點，頻率從大到小掃描時（向下掃頻），共振點小于實際共振點。由此可見，通過正弦掃頻振動試驗尋找試驗體的共振點時，有必要考慮掃頻速度和掃頻方向?qū)υ囼烍w響應的影響。引入一個無量綱參數(shù)η（下一篇文章說明），可以簡單的進行判斷。

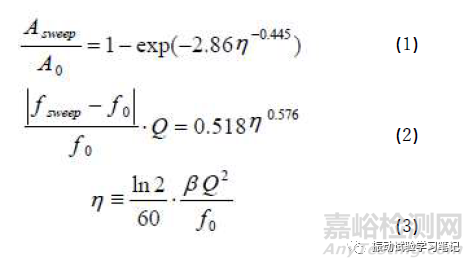
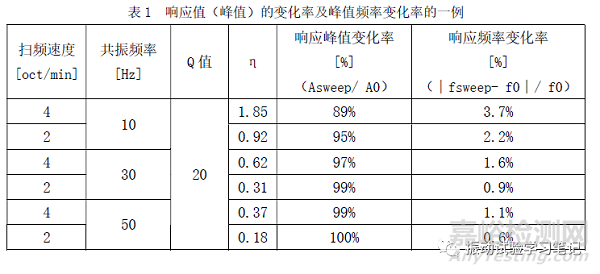
上面三式中，Asweep為振動響應峰值；A0為完全共振時的振幅；fsweep為振動響應峰值對應的峰值頻率；f0為試驗體的共振頻率；β為掃頻速度，單位oct/min；Q為試驗體的Q值。式（1）表示對應掃頻速度，振動響應峰值的變化率（Asweep/ A0）；式（2）是對應掃頻速度，振動響應的峰值頻率的偏移量（∣fsweep- f0∣·Q/f0）。這兩個公式是通過利用單自由度振動系統(tǒng)的過渡振動響應計算結(jié)果得到的擬合半經(jīng)驗公式（下一篇文章中和無量綱參數(shù)η一起介紹）。可以通過表1，某一試驗體的試驗結(jié)果來得到驗證。表1表明，通過掃頻試驗結(jié)果估算試驗體Q值和共振頻率時，會有百分之幾的誤差，需要引起注意。

綜上所述，振動臺利用頻率的變化激勵試驗體，通過試驗體的共振頻率（fn）達到共振狀態(tài)，與該共振的動態(tài)放大因子（Q）和激勵頻率本身的幅值有關外，還與掃頻速度有關。若掃頻速度選擇不合適，則試驗體的動態(tài)響應幅值可能達不到穩(wěn)定振動理論所預計的那么大。比如，掃頻速度過快，則共振頻率只是部分被激勵，或在極端情況下完全被漏掉。通常要保證達到靜態(tài)諧振曲線（掃頻速度為零）幅值的95%，見圖2，從諧振頻率的總振動次數(shù)，在衰減比小的情況下，應達到大于等于300個振動周期，即掃頻速度小于等于

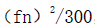
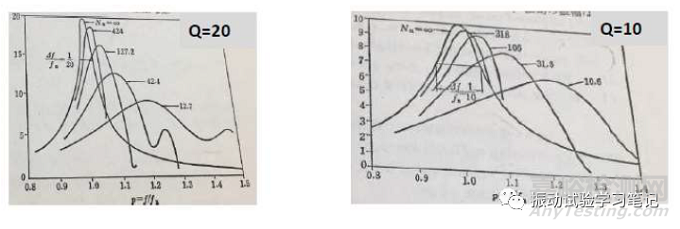
下圖是不同頻率對Q為20和10兩個單自由度系統(tǒng)所激起的共振狀態(tài)。圖中，橫坐標是理論共振頻率和實際共振頻率之比，可以看出振動次數(shù)Nn越小（相當于掃頻速度快），不僅系統(tǒng)被激起的共振響應幅值越小，而且顯示的共振頻率明顯高于理論共振頻率。在對數(shù)掃頻中尋找共振頻率的試驗中，如果共振沒有被激起，可以先檢查掃頻速度是否過快。但也需要避免不適當?shù)姆怕驗檎駝禹憫獧z查的時間是不能從功能試驗或耐久試驗的時間中扣除的。

穩(wěn)態(tài)正弦掃頻是最普遍的激振方法，借助激振設備對被測對象施加一個頻率可控的簡諧激振力，在掃描頻帶范圍內(nèi)具有連續(xù)頻譜，能激起該頻帶內(nèi)的所有振動模態(tài)。一般有線性掃頻和對數(shù)掃頻兩種方式，若所關心的結(jié)構(gòu)固有頻率范圍不大，可采用線性掃頻；對于固有頻率范圍較大的情況，可采用對數(shù)掃頻。掃頻速度的控制也很重要，若掃描太快，對于輕阻尼機構(gòu)，可能會遺漏一些模態(tài)，因此頻率變化要盡可能慢，以使系統(tǒng)響應達到穩(wěn)定狀態(tài)。為了避免響應滯后引起幅頻特性的峰值后移，可反復進行頻率向上和向下的掃頻激勵，并取多次測量的平均。這種激勵方式的優(yōu)點是激振功率大，能量集中、信噪比高，能保證響應測試的精度，信號的頻率和幅值易于控制，且當激振能量大小不同時，在非線性結(jié)構(gòu)中將產(chǎn)生不同的頻率響應函數(shù)，因而能檢測出系統(tǒng)的非線性程度。其缺點是測試時間長，特別是小阻尼結(jié)構(gòu)，不能通過平均消除非線性因素的影響，容易產(chǎn)生泄露誤差。

  讀到此處，理論基礎較差的讀者可能是一頭霧水，不知所云。少廢話，針對文章開頭的問題（在共振點探查試驗中，在沒有指定掃頻速度和掃頻方向時，不知道該如何選擇合適的掃頻速度和掃頻方向進行試驗？），有沒有行之有效的方法？有的，重點來了，根據(jù)作者多年的現(xiàn)場經(jīng)驗，只要記住以下的方法即可：在掃描頻率范圍內(nèi)，不快不慢剛剛好，建議加速度取2～5m/s2中的一個值（盡量取小，加速度太大，在不知道Q值的情況下，共振時容易損壞試驗體。），掃頻速度在1oct/min左右，共振點取向上向下掃頻的平均值，來回掃頻1-2次，共振點取響應的2-3倍。本方法使用至今，基本上都能解決現(xiàn)場的共振點探查問題，但不排除特殊情況。另外，在有試驗標準規(guī)定的場合下，請按照標準的規(guī)定執(zhí)行。