天堂网www,免费追剧大全在线观看电视剧,97久久精品无码一区二区欧美人 ,日本丰满少妇高潮呻吟

為啥要做顯著性分析？

簡單來說，當我們做實驗得到一堆數據后，得知道這些數據里呈現出的差異到底是真的有意義，還是只是偶然出現的波動。顯著性分析就像是一個“數據裁判”，能幫我們判斷不同組數據之間的差異是不是靠譜，讓我們的研究結論更有說服力。比如說，研究某種藥物對病癥的治療效果，通過顯著性分析，我們才能確定觀察到的病情改善是不是因為藥物起作用，而不是隨機因素導致的。

常用的顯著性分析方法

T 檢驗

• 適用場景：主要用于兩組數據的比較，像是比較實驗組和對照組的某個指標均值是否存在顯著差異。比如對比對照組和實驗處理組來明確處理是否有效果。

• 實現方式：在 R 語言中，使用t.test()函數就能輕松搞定。兩組數據group1和group2，代碼：t.test(group1, group2)，運行后就能得到 t 值、p 值等關鍵結果。

方差分析（ANOVA）

• 適用場景：當我們要比較三組及以上數據的均值差異時，方差分析就派上用場了。例如研究不同肥料對農作物產量的影響，有多種肥料類型的實驗組和一個對照組。

• 實現方式：R 語言里的aov()函數是常用工具。三組數據groupA、groupB、groupC，代碼為aov_result <- aov(response_variable ~ group_variable, data = your_data_frame)，其中response_variable是要分析的因變量（如農作物產量），group_variable是自變量（如肥料類型），然后通過summary(aov_result)查看分析結果。

卡方檢驗

• 適用場景：常用于分析分類數據的關聯性和獨立性。比如調查不同性別對某種產品的偏好是否存在顯著差異，性別和產品偏好就是兩個分類變量。

• 實現方式：在 R 中，chisq.test()函數。chisq.test(contingency_table)就能給出卡方值、自由度和 p 值等結果，讓我們判斷分類變量之間的關系是否顯著。

結果解讀

當得到顯著性分析的結果，重點關注 p 值哦。一般來說，如果 p 值小于設定的顯著性水平（常見的是 0.05），那就意味著數據中的差異是顯著的，研究假設可能是成立的；反之，如果 p 值大于 0.05，就說明差異可能不顯著，要謹慎下結論，也需要進一步優化實驗或者分析方法。

注意事項

• 數據獨立性：確保數據集中的每個觀測值都是獨立的，不然會嚴重影響分析結果的準確性。比如在抽樣調查時，不能有重復抽樣或者關聯性抽樣的情況。

• 樣本量合理性：樣本量過小可能導致檢測不出真實存在的差異，而樣本量過大可能會把微小的、無實際意義的差異也檢測出來。所以要根據研究目的和總體情況，合理確定樣本量。

• 數據分布假設：像 t 檢驗和方差分析通常要求數據滿足正態分布等假設條件，如果數據不滿足，可能需要先進行數據轉換（如對數轉換）或者選擇非參數檢驗方法，不然結果可能不準確哦。

如何進行顯著性差異abcd字母標注法？

一、顯著性分析

通常顯著性分析后三種標注差異結果的方式：1，用*標注；2，直接用P值標注；3，或用abcd標注。

第一種和第二種一般適應于組別較少的。

第三種組別多是，用abcd比較，又稱多重比較。

多重比較和兩兩比較是不一樣的。不能簡單理解為多重比較就是包含多個兩兩比較而已。因為（1）誤差由多個處理內的變異合并估計，自由度增大了，因而比較的精確度也增大了；（2）由于F測驗顯著，證實處理間總體上有真實差異后再做的兩兩平均數的比較，不大會想單獨比較是那樣蔣個別偶然性的誤差誤判為真實誤差。

二、abcd標注步驟

首先將全部平均數從大到小依次排列，然后在最大的平均數上標上字母a；

并將該平均數與以下各平均數相比，凡相差不顯著的，都標上字母a，直至某一個與之相差顯著的平均數，標記字母b；

再以該標有b的該平均數為標準，與上方各個比它大的平均數比較，凡不顯著的也一律標以字母b；再以標有b的最大平均數為標準，與以下各未標記的平均數比，凡不顯著的繼續標以字母b，直至遇到某一個與其差異顯著的平均數標記c。

凡有一個相同標記字母的即為差異不顯著,凡具不同標記字母的即為差異顯著.

小寫字母表示顯著水平α = 0.05；大寫字母表示顯著水平α = 0.01

舉個栗子：如何使用prism計算顯著性并標注字母

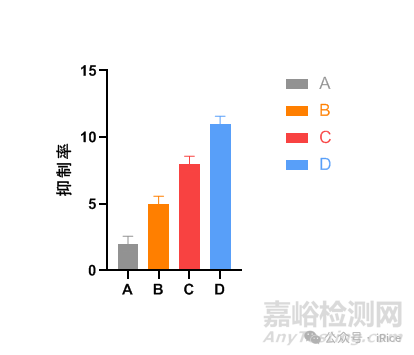
四個藥劑對病害真菌的抑制率比較

1，首先是輸入數據，然后點擊graphs生稱圖片

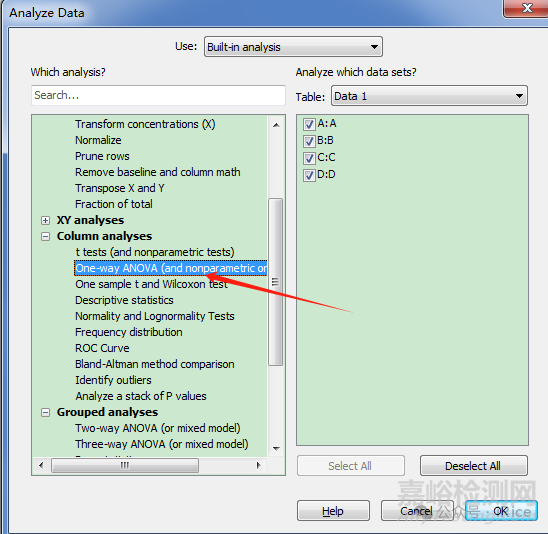
2，在result選擇中，選擇單因素方差分析

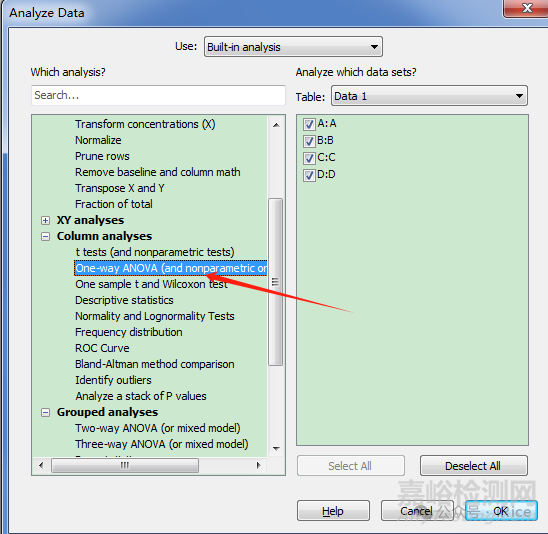
點擊ok后設置下比對參數

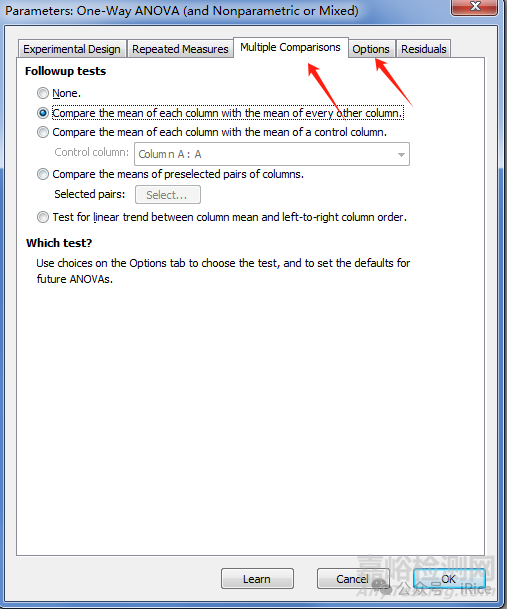
這里我們選擇是新復極差法。

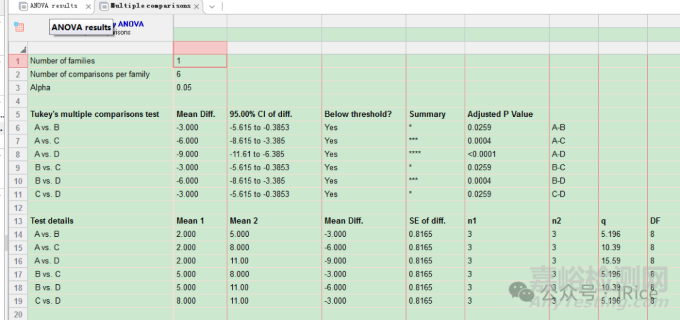
然后根據結果在圖中標注顯著性差異字母。

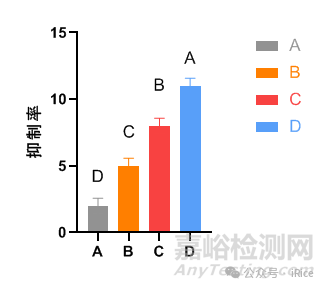
三、多重比較的方法

多重比較一般含有三種方法：最小顯著差數法，q檢驗和新復極差法。

LSD法（最小顯著差數法）：適用于一對或幾對在專業上有特殊意義的樣本均數間的比較。LSD法是最簡單的比較方法之一，它實際上只是t檢驗的一種簡單變形，未對檢驗水準做任何校正，只是在標準誤的計算上充分利用了樣本信息。

q檢驗：適用于多個樣本均數兩兩之間的全面比較。SNK-q檢驗是一種基于預先指定的準則將各組均值分為多個亞組，利用Studentized Range分布進行假設檢驗的方法，并根據所要檢驗的均值個數調整總的“棄真”錯誤概率不超過設定的顯著性水平a。

新復極差法：全稱為Tukey's Honestly Significant Difference法。應用這種方法要求各組樣本含量相同。Tukey法也是利用Studentized Range分布來進行各組均數間的比較，與SNK法不同的是，它控制所有比較中最大的“棄真”錯誤概率不超過設定的顯著性水平a。

選擇依據：

如果否認正確的（即犯α錯誤）是事關重大或后果嚴重的，應用q檢驗；這是寧愿使犯β錯誤的風險較大而不使犯α錯誤有較大風險的情況。

如果承受不正確的（即β錯誤）是事關重大或后果嚴重的，那么易采用PLSD（LSD的另一種形式）或SSR（最小顯著極差法）測驗，這是寧愿冒較大的α錯誤的風險，而不愿冒較大的β錯誤的風險的情況。

在一般的農業試驗研究中，較為廣泛應用的是PLSD測驗法和SSR測驗法。